The Datum Family Most Commonly Used in Gis in the Us Is:
Introduction
Comparing of these projections:
| Project | Blazon | Primal virtues | Comments |
|---|---|---|---|
| Stereographic | azimuthal | conformal | Created earlier 150 AD Best Used in areas over the Poles or for small scale continental mapping |
| Lambert Conformal Conic | conic | conformal | Created in 1772 Best Used in mid-latitudes – e.one thousand. The states, Europe and Australia |
| Mercator | cylindrical | conformal and true direction | Created in 1569 Best Used in areas around the Equator and for marine navigation |
| Robinson | pseudo-cylindrical | all attributes are distorted to create a 'more pleasant' appearance | Created in the 1963 Best Used in areas around the Equator |
| Transverse Mercator | cylindrical | conformal | Created in 1772 Best Used for areas with a n-s orientation |
Azimuthal Project – Stereographic
The oldest known record of this projection is from Ptolemy in nearly 150 AD. However it is believed that this projection was well known long before that time – probably every bit far back as the 2nd century BC.
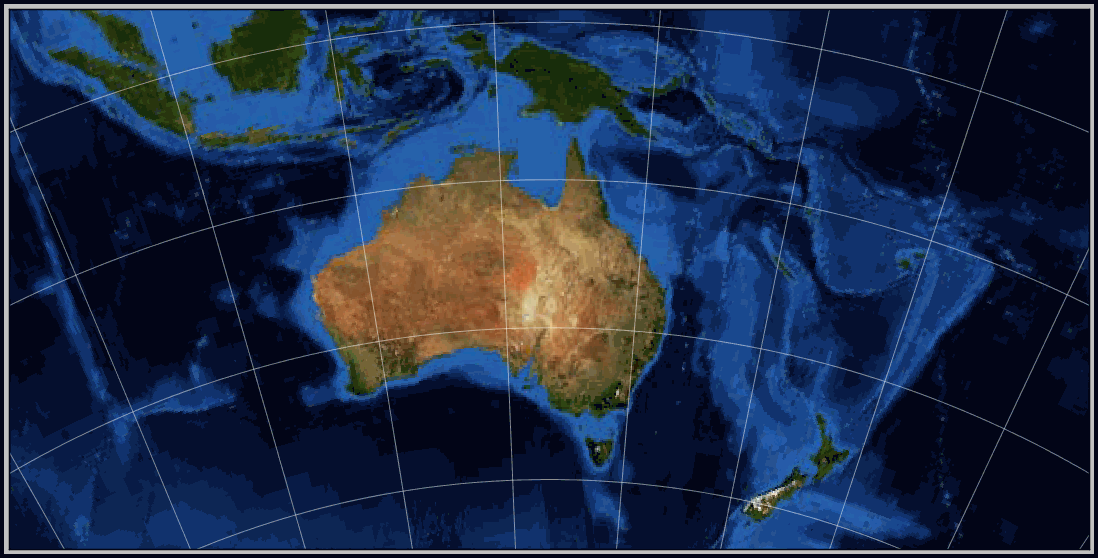
Today, this is probably one of the most widely used Azimuthal projections. It is near commonly used over Polar areas, but tin be used for small scale maps of continents such as Australia. The great attraction of the projection is that the Earth appears as if viewed form space or a globe.
This is a conformal projection in that shapes are well preserved over the map, although extreme distortions practice occur towards the edge of the map. Directions are true from the centre of the map (the bear upon bespeak of our imaginary 'piece of paper'), but the map is not equal-area.
I interesting feature of the Stereographic projection is that any straight line which runs through the centre point is a Cracking Circle . The advantage of this is that for a place of interest (e.g. Canberra, the uppercase city of Australia) a map which uses the Stereographic project and is centred on that identify of interest true distances can be calculated to other places of interest (e.g. Canberra to Sydney; or Canberra to Darwin; or Canberra to Wellington, New Zealand).
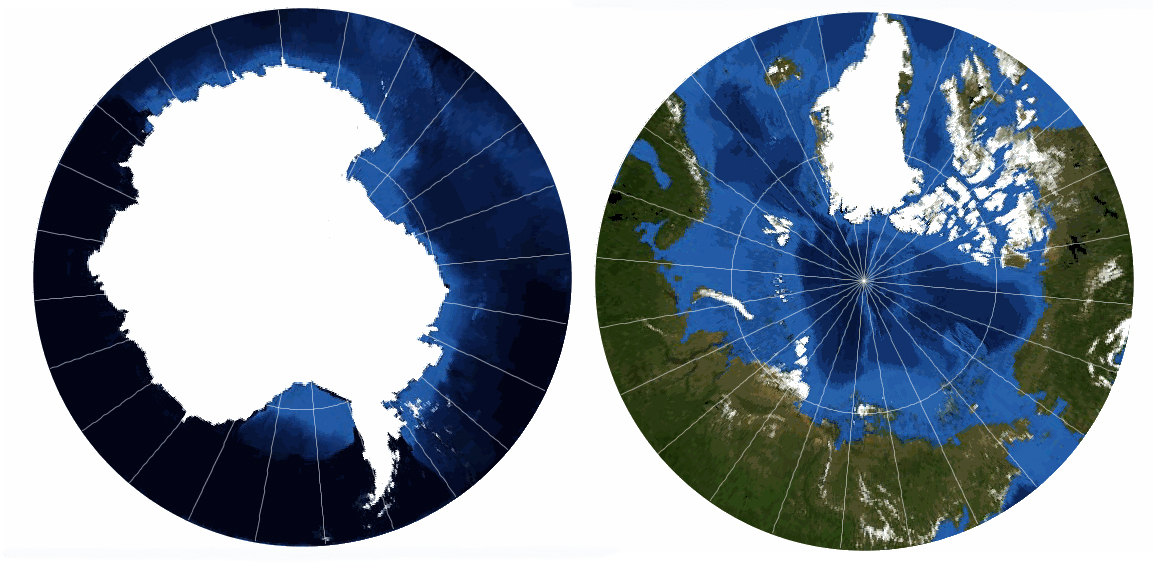
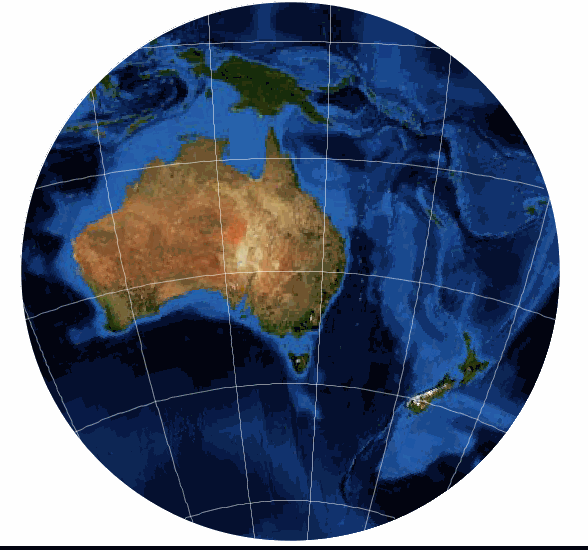
Conic Project – Lambert Conformal Conic
Johann Heinrich Lambert was a High german ⁄ French mathematician and scientist. His mathematics was considered revolutionary for its time and is all the same considered important today. In 1772 he released both his Conformal Conic projection and the Transverse Mercator Projection.
Today the Lambert Conformal Conic projection has go a standard projection for mapping big areas (small calibration) in the mid-latitudes – such as USA, Europe and Australia. It has also go specially popular with aeronautical charts such as the 1:100,000 scale World Aeronautical Charts map serial.
This project commonly used ii Standard Parallels (lines of latitudes which are unevenly spaced concentric circles).
The project is conformal in that shapes are well preserved for a considerable extent most to the Standard Parallels. For world maps the shapes are extremely distorted away from Standard Parallels. This is why it is very pop for regional maps in mid-latitude areas (approximately 20° to sixty° North and Southward).
Distances are only truthful forth the Standard Parallels. Across the whole map directions are generally true.
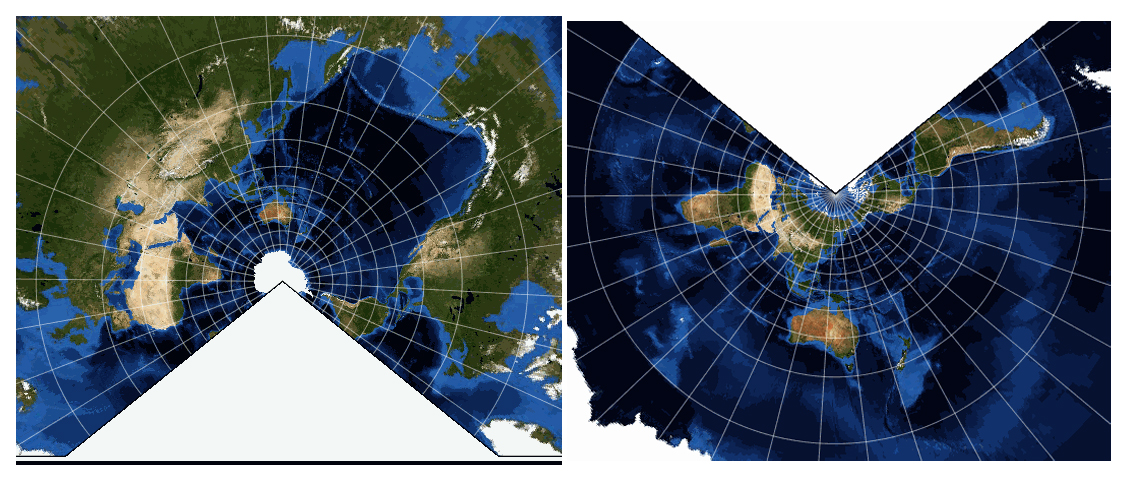
First map has standard Parallels at 30° and threescore° South and the second has standard Parallels at 30° and 60° North.
Cylindrical Projection – Mercator
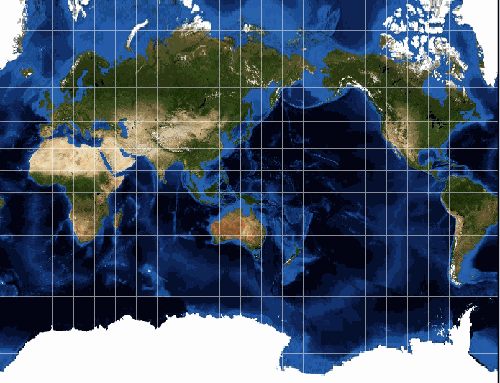
One of the most famous map projections is the Mercator, created by a Flemish cartographer and geographer, Geradus Mercator in 1569.
Information technology became the standard map projection for nautical purposes considering of its power to represent lines of constant true direction. (Constant true direction means that the straight line connecting whatsoever 2 points on the map is the same direction that a compass would testify.) In an era of sailing ships and navigation based on direction only, this was a vitally important characteristic of this project.
The Mercator Projection e'er has the Equator equally its Standard Parallel. Its construction is such that the lines of longitude and latitude are at right angles to each other – this ways that a world map is always a rectangle.
Also, the lines of longitude are evenly spaced autonomously. But the altitude between the lines of latitude increment away from the Equator. This human relationship is what allows the direction betwixt whatever two points on the map to be constant true direction.
While this relationship betwixt lines of lines of latitude and longitude correctly maintains direction, information technology allows for distortion to occur to areas, shapes and distances. Nearest the Equator there is little distortion. Distances along the Equator are e'er correct, but nowhere else on the map. Between about fifteen° n and south the areas and shapes are well preserved. Further out (to about l° north and south) the areas and shapes are reasonably well preserved. This is why, for uses other than marine navigation, the Mercator projection is recommended for use in the Equatorial region only.
Despite these distortions the Mercator projection is more often than not regarded every bit existence a conformal projection. This is because within minor areas shapes are essentially true.
See also Transverse Mercator and Universal Transverse Mercator below.
Cylindrical Project – Robinson
In the 1960s Arthur H. Robinson, a Wisconsin geography professor, developed a project which has go much more popular than the Mercator projection for world maps. Information technology was developed considering modernistic map makers had become dissatisfied with the distortions inherent in the Mercator project and they wanted a world projection which 'looked' more like reality.
In its time, the Robinson project replaced the Mercator projection as the preferred projection for globe maps. Major publishing houses which accept used the Robinson project include Rand McNally and National Geographic.
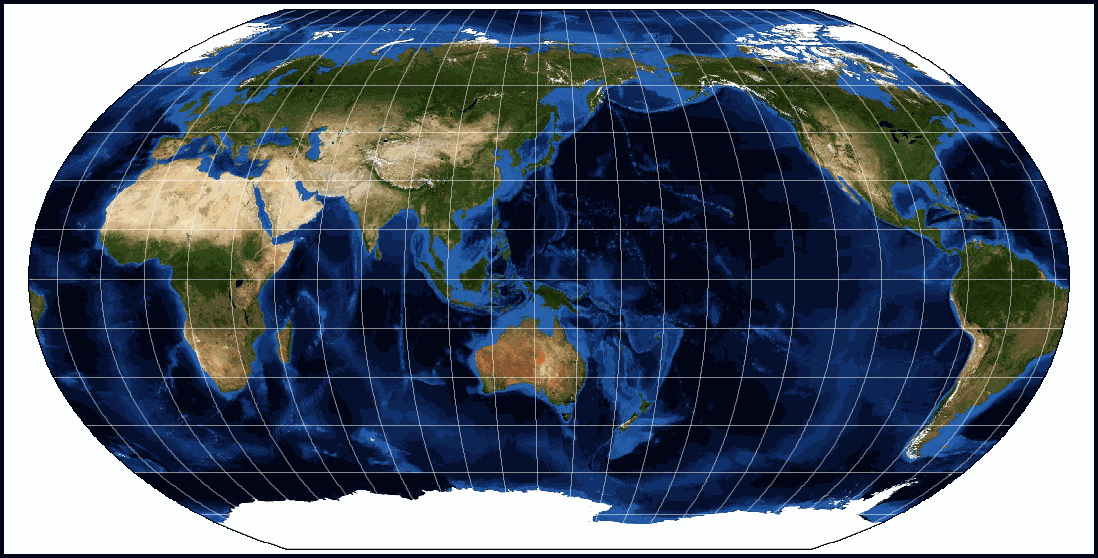
Equally it is a pseudo-cylindrical projection, the Equator is its Standard Parallel and it still has like distortion bug to the Mercator projection.
Between about 0° and 15° the areas and shapes are well preserved. However, the range of acceptable distortion has been expanded from approximately fifteen° north and south to approximately 45° north to southward. As well, at that place is less distortion in the Polar regions.
Dissimilar the Mercator projection, the Robinson projection has both the lines of distance and longitude evenly spaced beyond the map. The other significant difference to the Mercator is that but the line of longitude in the centre of the map is straight (Key Meridian), all others are curved, with the corporeality of curve increasing away from the Key Pinnacle.
In opting for a more pleasing appearance, the Robinson projection 'traded' off distortions – this projection is neither conformal, equal-area, equidistant nor true management.
Cylindrical Projection – Transverse Mercator
Johann Heinrich Lambert was a German ⁄ French mathematician and scientist. His mathematics was considered revolutionary for its time and is notwithstanding considered important today. In 1772 he released both his Conformal Conic projection and the Transverse Mercator projection.
The Transverse Mercator projection is based on the highly successful Mercator project. The main forcefulness of the Mercator projection is that it is highly accurate most the Equator (the 'touch point' of our imaginary slice of paper – otherwise chosen the Standard Parallel) and the main trouble with the projection is that distortions increment away from the Equator. This set of virtues and vices meant that the Mercator projection is highly suitable for mapping places which have an east-west orientation near to the Equator but not suitable for mapping places which have are north-southward orientation (eg South America or Republic of chile).
Lambert's stroke of genius was to change the way the imaginary piece of paper touched the Globe… instead of touching the Equator he had it touching a line of Longitude (any line of longitude). This touch betoken is called the Fundamental Peak of a map. This meant that accurate maps of places with northward-south orientated places could now be produced. The map maker only needed to select a Central Meridian which ran through the eye of the map.
A Special Example – Universal Transverse Mercator System (UTM)
It took some other 200 years for the next development in take identify for the Mercator projection.
Over again, like Lambert's revolutionary modify to the fashion that the Mercator project was calculated; this development was a alter in how the Transverse Mercator projection was used. In 1947 the North Atlantic Treaty Organization (NATO) adult the Universal Transverse Mercator coordinate organisation (generally merely called UTM).
NATO recognised that the Mercator/Transverse Mercator projection was highly accurate along its Standard Parallel/Central Meridian. Indeed as far every bit 5° away from the Standard Parallel ⁄ Central Meridian at that place was minimal distortion.
Like the World Aeronautical Charts, the UTM arrangement was able to build on the achievements of the International Map of the World. Equally well as developing an agreed, international specification the IMW had adult a regular grid system which covered the unabridged Surface of the Earth. For low to mid-latitudes (0° to sixty° North and Due south) the IMW established a grid organization that was half-dozen° of longitude wide and four° of latitude high.
Using this NATO designed a like regular system for the Earth whereby it was divided into a series of half dozen° of longitudinal wide zones. In that location are a total of lx longitudinal zones and these are numbered 1 to 60 – east from longitude 180° . These extend from the North Pole to the Southward Pole. A central tiptop is placed in middle of each longitudinal zone. Equally a outcome, within a zone nothing is more than than 3° from the central meridian and therefore locations, shapes and sizes and directions between all features are very accurate.
Please annotation that this is not a new ⁄ revised projection, just a series of maps using the same project (Transverse Mercator). This is not unremarkably appreciated and UTM is frequently wrongly described as a projection in its own correct – it is not – information technology is a projection arrangement.
This is why UTM is regarded equally a Special Instance.
The shortcoming in the UTM organisation is that between these longitude zones directions are not true – this trouble is overcome by ensuring that maps using the UTM system do non comprehend more than one zone.
World wide, including Commonwealth of australia, this UTM organization is used by mapping agencies for local and national, topographic maps.
UTM Zones
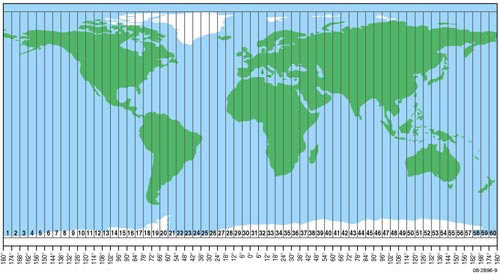
As already noted, the UTM system involves a serial of longitudinal zones which are 6° broad and numbered ane to threescore – e from longitude 180°.
Still, different the International Map of the World (IMW) the UTM system opted to use latitudinal zones which were twice as wide – i.eastward. eight° of breadth wide. In that location are 20 of these and they are numbered A to Z (with O and I non being used) – north from Antarctica. Like the IMW organisation each characteristic on the Earth is now able to be described based on the UTM grid it is located in. Ane confusing detail is that these grid cells are variably called a UTM zone.
For example, in the example of Sydney, Australia, its UTM grid jail cell (zone) would be identified as:
- H – for the latitudinal zone information technology belongs to
- 56 – for the longitudinal zone it belongs to
Add the ii together – the UTM grid zone (grid jail cell) which contains Sydney is 56H
UTM Map grid and the Australian Map Grid
As is explained in the section tiled Explaining Some Jargon – Graticules and Grids there is a meaning deviation betwixt the 2.
- Graticules are lines of Longitude and Latitude. These never form a square or rectangular shape and their shape changes dramatically from the Equator to the Pole – from being close to square shaped to being close to triangle shaped.
- Grids are a regularly shaped overlay to a map. They are usually square, but they may exist rectangular.
Grids rarely run parallel to lines of Longitude and Breadth.
Likewise ease of use, there is another advantage to a filigree – on any given map it always covers the same amount of the Globe's surface. This is not truthful of a graticule organisation! A 1° x1° block of latitude and longitude near the Equator will always cover vastly more of the Earth's surface and a i° x1° block closer to a Pole. Therefore it is easy to measure distances using a grid – it removes the foibles of distortions inherent in each map projection.
When NATO created the UTM system it recognised this fact and built a filigree system into it. This involves a regular and circuitous arrangement of letters to identify grid cells. To identify individual features or locations distances are first measured from the west to the feature and and so measured from the south to the feature. The three are combined to give a precise location – based on the map grid.
Explaining some jargon:
- The Australian Map Grid (AMG) is the map grid which had been developed as part of the UTM organisation to all-time arrange Australian needs.
- Northings – these are the horizontal parallel lines of the filigree – i.e. they are serial of lines which run from the w to the eastward (like to lines of latitude – merely not the aforementioned). Their values increment towards the north.
- Eastings – these are the vertical parallel lines of the grid – i.e. they are series of lines which run from the northward to southward (similar to lines of longitude – merely not the same). Their values increase towards the eastward.
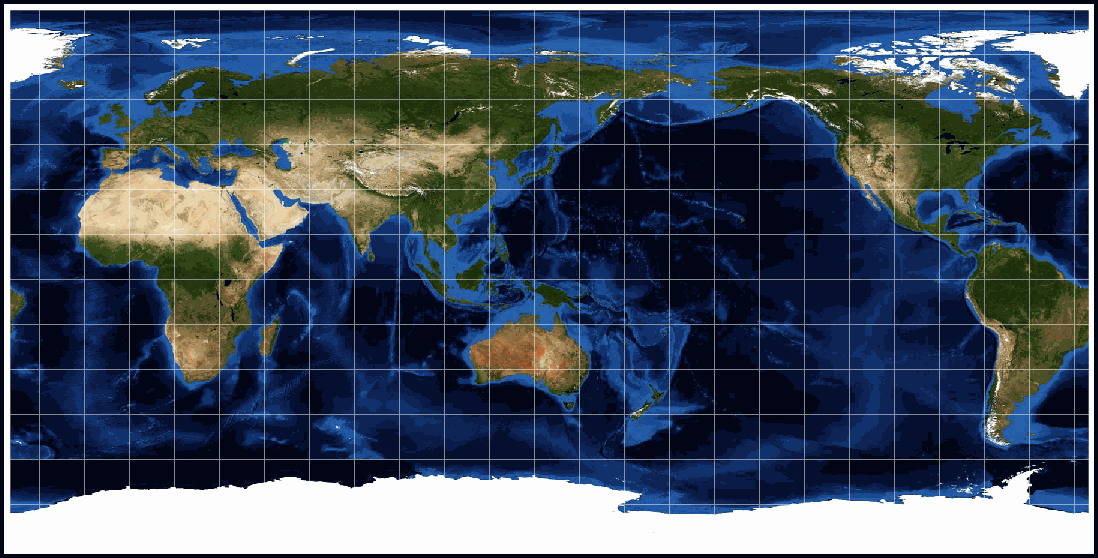
A Special Case – Geographic (or Plate Carrée)
This is a mathematically simple projection. It is also an aboriginal projection (maybe adult by Marinus of Tyre in 100).
Because of its simplicity it was usually used in the past (before computers allowed for very complex calculations) and it has been adopted equally the project of choice for use in computer mapping applications – notably Geographic Information Systems (GIS) and on web pages. Also, once again considering of its simplicity, information technology is equally able to be used with world and regional maps.
Plate Carrée is the French term for flat square. In GIS operations this projection is commonly referred to as Geographicals.
This is a cylindrical project, with the Equator equally its Standard Parallel. The difference with this project is that the latitude and longitude lines intersect to form regularly sized squares. By way of comparing, in the Mercator and Robinson projections they course irregularly sized rectangles.
While nosotros have described the Geographic or Plate Carrée as a projection, there is some debate as to whether it should exist considered to be a project. This is because it makes no endeavor to compensate for distortions due to the transfer of information from the surface of the Earth onto a 'flat slice of paper' (our map).
This is why we are describing the Geographical project as a Special Example.
Refer to the section on Projections for more information about distortions generated by projections.
Farther Reading
- Paul B. Anderson FCCS (USN, Retired) Old Dominion Academy Geography Department, GIS Pedagogy Assistant Kingsport – Map Projections
- http://www.csiss.org/map-projections/index.html/
- http://www.galleryofmapprojections.com/images/Aust_Centered_2009.jpg
- http://world wide web.galleryofmapprojections.com/gedymin/gedymin_prof_11x17.pdf
- Carlos A Furuti – Map Projections
- http://world wide web.progonos.com/furuti/MapProj/
- (The states) National Atlas Map Projections
- From Spherical Earth to Flat Map
harwardbacturter46.blogspot.com
Source: https://www.icsm.gov.au/education/fundamentals-mapping/projections/commonly-used-map-projections
0 Response to "The Datum Family Most Commonly Used in Gis in the Us Is:"
Post a Comment